SolveConPython

La función sigmoide es uno de los conceptos matemáticos más importantes en redes neuronales y machine learning.
En este artículo la vamos a explicar sin saltos, sin suposiciones previas y siempre conectando la matemática con código Python real.

Este será el primer bloque de una serie donde, al final, podrás construir una red neuronal completa uniendo piezas pequeñas y comprensibles.

¿Qué problema resuelve la función sigmoide?

En una red neuronal, muchas operaciones producen un número cualquiera:

• 3.7
• −12
• 0.04
• 8.9

Pero en muchos casos (por ejemplo, clasificación binaria) queremos probabilidades, es decir, valores entre 0 y 1:

• ¿Es spam o no?
• ¿Es fraude o no?
• ¿Pertenece a la clase A o no?

La función sigmoide toma cualquier número real y lo transforma en un valor entre 0 y 1.

La fórmula matemática de la sigmoide

La función sigmoide se define así:$$\sigma(x) = \frac{1}{1 + e^{-x}}$$σ(x)=1+e−x1​

No necesitas memorizarla ahora. Lo importante es entender qué hace:

• Si x es muy grande → el resultado se acerca a 1
• Si x es muy pequeño (negativo) → el resultado se acerca a 0
• Si x = 0 → el resultado es 0.5

Intuición visual: la curva en forma de “S”

La sigmoide genera una curva suave con forma de S:

• A la izquierda: valores cercanos a 0
• En el centro: transición gradual
• A la derecha: valores cercanos a 1

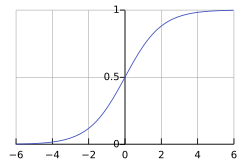
Esta forma es clave porque permite que una red neuronal aprenda gradualmente, no con saltos bruscos.

Implementar la sigmoide en Python

Ahora pasemos directamente al código.

import numpy as np
def sigmoid(x):
    return 1 / (1 + np.exp(-x))

Eso es todo.
Esta función acepta:

• un número (float)
• una lista
• un array de NumPy

Y devuelve el resultado elemento por elemento.

Ejemplo rápido

sigmoid(0)
# 0.5
sigmoid(5)
# ~0.993
sigmoid(-5)
# ~0.0067

Dibujar la sigmoide con Python

Ver la curva ayuda mucho a entenderla.

import numpy as np
import matplotlib.pyplot as plt
def sigmoid(x):
    return 1 / (1 + np.exp(-x))
x = np.linspace(-10, 10, 400)
y = sigmoid(x)
plt.plot(x, y)
plt.axvline(0)
plt.axhline(0.5)
plt.title("Función sigmoide")
plt.xlabel("x")
plt.ylabel("σ(x)")
plt.show()

Observa:

• El punto central está en x = 0
• El valor allí es exactamente 0.5

¿Por qué la sigmoide es tan usada en redes neuronales?

Hay tres razones clave:

1. Convierte números en probabilidades
2. Es suave y derivable (muy importante para aprender)
3. Responde más fuerte cerca de 0, donde el modelo es más “incierto”

Eso nos lleva al siguiente punto.

La derivada de la sigmoide (sin miedo)

Cuando una red neuronal aprende, ajusta sus pesos usando derivadas.
La derivada de la sigmoide es sorprendentemente simple:$$\sigma'(x) = \sigma(x) \cdot (1 – \sigma(x))$$σ′(x)=σ(x)⋅(1−σ(x))

Esto significa algo muy práctico:

Si ya calculaste la sigmoide, no necesitas más exponenciales para su derivada.

Código de la derivada

def sigmoid_derivative(sigmoid_output):
    return sigmoid_output * (1 - sigmoid_output)

Más adelante, esta función será clave para backpropagation.

Nota importante: estabilidad numérica

Para valores muy grandes o muy pequeños, exp() puede causar problemas numéricos.
Una versión más estable sería:

def sigmoid_stable(x):
    x = np.asarray(x, dtype=float)
    out = np.empty_like(x)
    pos = x >= 0
    neg = ~pos
    out[pos] = 1 / (1 + np.exp(-x[pos]))
    exp_x = np.exp(x[neg])
    out[neg] = exp_x / (1 + exp_x)
    return out

Para aprender, la versión simple es suficiente.
Para producción, la versión estable es preferible.

Pieza reutilizable (guárdala)

Esta función será usada tal cual en la red neuronal completa:

def sigmoid(x):
    return 1 / (1 + np.exp(-x))

En artículos posteriores la usaremos así:

y_hat = sigmoid(z)

Qué viene después

En el Artículo #2 construiremos el siguiente bloque fundamental:

La neurona: suma ponderada + sesgo
Matemática: $z = XW + b$z=XW+b
Python: operaciones vectorizadas con NumPy

Código Python del artículo

Todo el código mostrado en este artículo está disponible en GitHub, listo para ejecutar y modificar.

👉 Código de este artículo: https://github.com/Benard-Kemp/la-funcion-sigmoide-en-Python

Incluye:

• Scripts en Python
• Ejemplos completos
• Código organizado por artículo

Te recomendamos clonar el repositorio y experimentar con los valores.